Kreistangenten
Berechnet werden die Gleichungen der folgenden Tangenten an einen bzw. zwei Kreise. Die Konstruktionen werden gezeichnet und bei Bedarf werden die Konstruktionslinien eingeblendet.
- Die Tangente an einen Kreis k in einem Punkt B
- Die Tangenten an einen Kreis k durch einen Punkt P außerhalb des Kreises
- Die Tangenten an einen Kreis k parallel zu einer Geraden g
- Die Tangenten an zwei Kreise k1 und k2
Beispiel 1:
Gegeben: ¯¯¯¯¯¯¯¯ k : M(5 | 8) , r =8,48528 , B(-1 | 2) Tangente an k in B ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t: x + y = 1
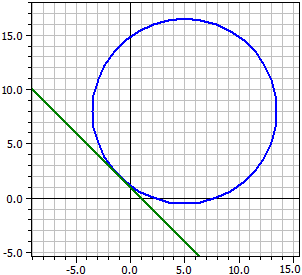
Beispiel 2:
Gegeben: ¯¯¯¯¯¯¯¯ k : M(5 | 8) , r =5 , P(-1 | 2) Tangenten an k durch P ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t1: 1,06014·x − 6,77319·y = -14,6065 t2: 6,77319·x − 1,06014·y = -8,89348 Berührpunkte ¯¯¯¯¯¯¯¯¯¯¯ k ∩ t1 = B1(5,77319|3,06014) k ∩ t2 = B2(0,0601439|8,77319)
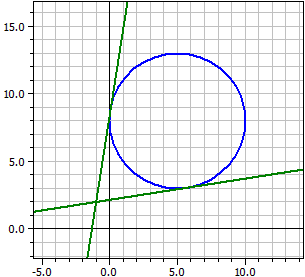
Beispiel 3:
Gegeben: ¯¯¯¯¯¯¯¯ k : M(5 | 8) , r =5 , g : x − 3·y = 0 Tangenten an k parallel zu g ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t1: x − 3·y = -3,18861 t2: x − 3·y = -34,8114 Berührpunkte ¯¯¯¯¯¯¯¯¯¯¯ k ∩ t1 = B1(6,58114|3,25658) k ∩ t2 = B2(3,41886|12,7434)
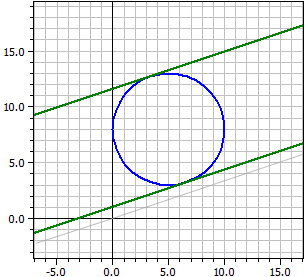
Beispiel 4:
Gegeben: ¯¯¯¯¯¯¯¯ k1 : M(5|8) , r =5 k2 : M(-1|2) , r =3 Äußere Tangenten ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t1: -4,2923·x + 7,04104·y = -6,36427 t2: -7,04104·x + 4,29230·y = 40,3643 Innere Tangenten ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t3: 1,21895·x + 2,55228·y = 12,3709 t4: -2,55228·x − 1,21895·y = -8,3709
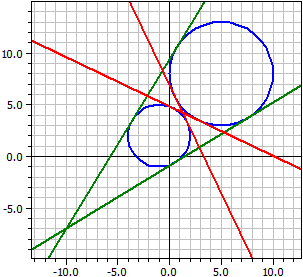
Siehe auch:
Einstellen der GrafikWikipedia: Kreistangente

