Kreistangenten-Konstruktion
Die Legende auf der rechten Seite der Grafik dient neben der farblichen Unterscheidung der Tangenten gleichzeitig als Schalter, mit denen die Konstruktiosnlinien ein- bzw. ausgeblendet werden können.
Die Tangente an einen Kreis k in einem Punkt B

Grundlage für die Konstruktionen ist, dass die Tangente eines Kreises senkrecht zum Berührungsradius verläuft. Man zeichnet also die Gerade durch M und B und konstruiert die dazu senkrechte Gerade durch B.
Die Tangenten an einen Kreis k durch einen Punkt P außerhalb des Kreises
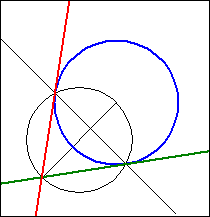
Die Berührpunkte B1 und B2 der Tangenten erhält man als Schnittpunkte des Thales-Kreises über der Strecke MP mit dem Kreis k.
Die Geraden (P B1) und (P B2) sind die gesuchten Tangenten.
Die zusätzlich eingezeichnete Gerade (B1B2) ist die Polare von P, die wir bei der Berechnung der Tangentengleichungen verwendet haben.
Die Tangenten an einen Kreis k parallel zu einer Geraden g
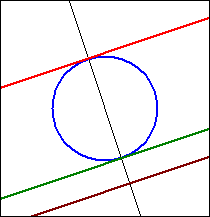
Die Berührpunkte B1 und B2 der Tangenten erhält man als Schnittpunkte der Lotgeraden von M auf g mit dem Kreis k.
Die Parallelen zu g durch B1 und B2 sind die gesuchten Tangenten.
Die gemeinsamen Tangenten an zwei Kreise k1 und k2
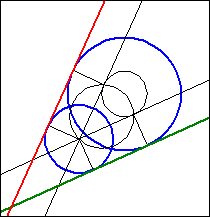
Um die äußeren Tangenten an zwei Kreise k1(M1,r1) und
k2(M2,r2) zu konstruieren, zeichnet man zunächst einen Kreis k3 um M1
mit Radius r3=r1−r2.
Seine Schnittpunkte S1 und S2 mit dem Thales-Kreis über der Strecke
M1M2 sind die Berührpunkte von zwei Tangenten, die man von M2 an den Kreis k3
legen kann.
Die Halbgeraden von M1 durch S1 bzw. S2 schneiden den Kreis
k1 in den Berührpunkten der gesuchten äußeren Tangenten. Diese sind parallel zu den Tangenten an den Hilfskreis k3.

Liegt k2 ganz außerhalb von k1, so existieren zusätzlich zwei "innere" Tangenten, die sich zwischen den Kreisen kreuzen.
Um die inneren Tangenten an zwei Kreise k1(M1,r1) und
k2(M2,r2) zu konstruieren, zeichnet man zunächst einen Kreis k3 um M1
mit Radius r3=r1+r2.
Seine Schnittpunkte S1 und S2 mit dem Thales-Kreis über der Strecke
M1M2 sind die Berührpunkte von zwei Tangenten, die man von M2 an den Kreis k3
legen kann.
Die Halbgeraden von M1 durch S1 bzw. S2 schneiden den Kreis
k1 in den Berührpunkten der gesuchten inneren Tangenten. Diese sind parallel zu den Tangenten an den Hilfskreis
k3.
Siehe auch:
Einstellen der Grafik
Wikipedia: Kreistangente |
Pol und Polare

