Kreis und Kreisteile

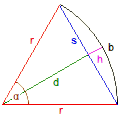
Sind zwei der folgenden Größen eines Kreissektors gegeben, so werden die anderen berechnet:

• Radius r
• Bogen b
• Sehne s
• Abstand d
• Pfeilhöhe h
• Fläche des Kreissektors A1
• Mittelpunktswinkel α

Außerdem werden die Fläche des Kreissegments, die Kreisfläche und der Kreisumfang berechnet.

Beispiel:

Gegeben:
¯¯¯¯¯¯¯¯
                 Bogen b = 1
                Winkel α = 45°

Ergebnisse :
¯¯¯¯¯¯¯¯¯¯
                Radius r = 1,2732395
                Sehne s = 0,97449536
      Kreissektor A1 = 0,63661977
             Abstand d = 1,17632
           Pfeilhöhe h = 0,096919589
  Kreissegment A2 = 0,063460604

         Kreisfläche A = 5,0929582
      Kreisumfang u = 8

Anwendung:

Zu einem Bruchstück eines Tellers soll die Größe des ursprünglichen Tellers berechnet werden. Gemessen werden eine Sehne s und die zugehörige Sagitta oder Pfeilhöhe h.

Gegeben:
¯¯¯¯¯¯¯¯
                Sehne s = 21
           Pfeilhöhe h = 6

Ergebnisse:  
¯¯¯¯¯¯¯¯¯¯
               Radius r = 12,1875
               Winkel α = 118,97953°  
               Bogen b = 25,308373
     Kreissektor A1 = 154,2229
            Abstand d = 6,1875
 Kreissegment A2 = 89,254148

        Kreisfläche A = 466,63696
     Kreisumfang u = 76,576321

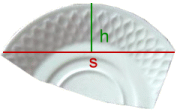
Der Teller hatte also einen Radius von 12,2cm.

Siehe auch:

Einstellen der Grafik
Wikipedia: Kreissektor | Kreissegment