Distances sur la sphère
La distance entre deux points P1 et P2 sur une sphère est calculée par combinéer certains fonctions de MatheAss.
Les données GPS (latitude et longitude) des deux points sont saisies. Avec le rayon de la sphère, ils donnent les coordonnées polaires des points.
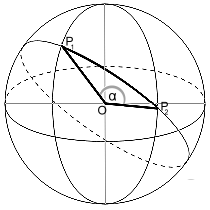
Celles-ci sont converties en leurs coordonnées cartésiennes avec la fonction correspondante de MatheAss . Le résultat fournit les coordonnées de leurs vecteurs de position dans un système de coordonnées avec le centre de la sphère comme origine.
Avec son produit scalaire on obtient l'angle α entre les deux vecteurs et enfin, comme produit de α en radians avec le rayon de la sphére, la longueur de l'arc de cercle sur la sphère.
Exemple:
À vol d'oiseau entre l'Alexanderplatz à Berlin et l'hôtel de ville de New York.
La terre est idéalisée comme une sphère d'un rayon de 6371 km.
GPS décimal
¯¯¯¯¯¯¯¯¯¯¯
Berlin : 52.523403, 13.411400
New York : 40.714268, -74.005974
GPS dms
¯¯¯¯¯¯¯
Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E
New York : 40° 42' 51.3648" N, 74° 0' 21.5064" O
Coordonnées polaires
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlin : (6371 | 13.411400° | 52.523403°)
New York : (6371 |-74.005974° | 40.714268°)
Coordonnées cartésiennes
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlin : (3770.6450 | 899.08721 | 5056.0379)
New York : (1330.5796 |-4642.1091 | 4155.7216)
Vecteurs de position
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 3770,645048 ⎫ -> ⎧ 1330,57957098 ⎫
a = ⎪ 899,087213119 ⎪ b = ⎪-4642,10910614 ⎪
⎩ 5056.03788605 ⎭ ⎩ 4155.72160425 ⎭
-> ->
α = arccos( a · b / r2 )
= 1,002215 [rad] = 57,422692°
Distance
¯¯¯¯¯¯¯¯
d = · α [rad] = 6385,112
Saisie des données GPS
Les données GPS peuvent être saisies en degrés décimales ainsi qu'en degrés, minutes et secondes.
Les deux représentations sont sorties.

Le programme est donc également adapté pour convertir les degrés décimales en degrés, minutes et secondes (dms) et vice versa.

