Systèmes de coordonnées
Avec ce programme, on peut convertir des coordonnées cartésiennes tridimensionnelles au coordonnées polaires (coordonnées sphériques) ou coordonnées cylindriques et vice versa.
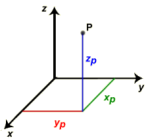
Coordonnées cartésiennes
Les coordonnées cartésiennes (x|y|z) d'un point correspondes à un système de coordonnées avec des axes orthogonaux et avec la même mesure sur chaque xe.
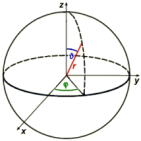
Coordonnées polaires
Les coordonnées polaires (r|φ|Θ) d'un point signifies sa distance r à l'origine, l'angle de rotation φ (phi) dans la section équatoriale et l'angle d'élévation Θ (Theta) sur la sectionne équatoriale.
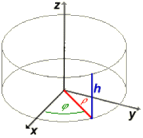
Coordonnées cylindriques
Les coordonnées cylindriques (ρ|φ|z) d'un point signifies sa distance ρ (rho) à l'axe de cylindre, l'angle de rotation φ (phi) autour de l'axe et l'hauteur z sur l'origine.
Exemple:
cartésiennes polaires cylindriques x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Avec z = 0 ou Θ = 0 on reçu des coordonnées bidimensionnelles.

