Distancias en la esfera
Se calcula la distancia entre dos puntos P1 y P2 en una esfera. Se combinan varias funciones de MatheAss.
Se ingresan los datos GPS (latitud y longitud) de los dos puntos. Junto con el radio de la esfera, dan las coordenadas polares de los puntos.
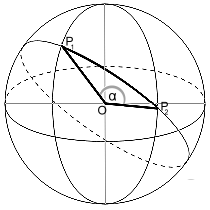
Estos se convierten en sus coordenadas cartesianas con la función correspondiente de MatheAss . El resultado proporciona las coordenadas de sus vectores de posición en un sistema de coordenadas con el centro de la esfera como origen.
Con su producto escalar se obtiene el ángulo α entre los dos vectores y finalmente, como el producto de α en radianes por el radio esférico, la longitud del arco circular sobre la esfera.
Ejemplo:
En línea recta entre Alexanderplatz en Berlín y el City Hall de Nueva York.
La tierra está idealizada como una esfera con un radio de 6371 km.
GPS decimal
¯¯¯¯¯¯¯¯¯¯¯
Berlín: 52.523403, 13.411400
Nueva York: 40.714268, -74.005974
GPS dms
¯¯¯¯¯¯¯
Berlín: 52° 31' 24.2508" N, 13° 24' 41.0400" E
Nueva York: 40° 42' 51.3648" N, 74° 0' 21.5064" W
Coordenadas polares
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlín: (6371 | 13,411400° | 52,523403°)
Nueva York: (6371 |-74,005974° | 40,714268°)
Coordenadas cartesianas
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlín: (3770,6450 | 899,08721 | 5056,0379)
Nueva York: (1330,5796 |-4642,1091 | 4155,7216)
Vectores de posición
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 3770,645048 ⎫ -> ⎧ 1330,57957098 ⎫
a = ⎪ 899,087213119 ⎪ b = ⎪-4642,10910614 ⎪
⎩ 5056.03788605 ⎭ ⎩ 4155.72160425 ⎭
-> ->
α = arccos( a · b / r2 )
= 1,002215 [rad] = 57,422692°
Distancia
¯¯¯¯¯¯¯¯¯
d = r · α [rad] = 6385,112
Ingresando datos GPS
Los datos del GPS se pueden ingresar en decimales, así como en grados, minutos y segundos.
Se dan salida a ambas representaciones.

Por lo tanto, el programa también es adecuado para convertir grados decimales en grados, minutos y segundos (dms) y viceversa.

