Sistemas de coordinados
Con esto puede transformar coordenadas cartesianas tridimensionales en coordenadas polares tridimensionales o coordenadas cilíndricas y viceversa.
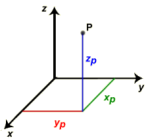
Coordenadas cartesianos:
En un sistema de coordenadas cartesianos (x | y | z) un punto se ubica por su distancia de cada una de las tres líneas de intersección perpendiculares entre sí con la misma unidad de longitud.
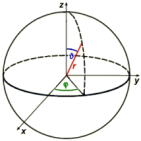
Coordenadas polares:
En un sistema de coordenadas polares (r | φ | Θ) un punto se ubica por su vector de radio, el ángulo de rotación φ (phi) en el plano ecuatorial y el ángulo de elevación Θ (Theta) desde el plano ecuatorial.
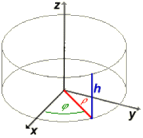
Coordenadas cilíndricos:
En un sistema de coordenadas cilíndricos (ρ | φ | z), un punto se ubica por su distancia ρ (rho) del eje del cilindro, el ángulo de rotación φ (phi) alrededor del eje y la altitud z sobre el origen.
Ejemplo:
cartesiano polar cilíndrico x = 1 r = 1,7320508 ρ = 1,4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1

