Integral Calculus

The oriented and the absolute content of the area between two function curves in a desired interval, i.e. the two integrals, are calculated

Also are determined:

• the twisting moments for rotation around x-, respectively y-axis,
• the bodies of revolution covered, and
• the arc lengths in the interval [a; b] and
• the center of gravity of the area (if A1=A2).

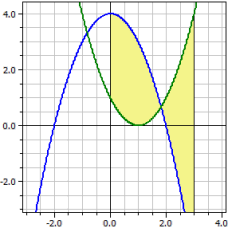
Example 1:

  ƒ1(x) = 4-x^2
  ƒ2(x) = (x-1)^2

  Interval from von  0  to  3

  Oriented content       :  A1 = 0,00000
  Absolute content       :  A2 = 9,50675

  Twisting moments    :  Mx = 9                  My = -9

  Bodies of revolution :  Vx = 56,5487        Vy = -56,5487

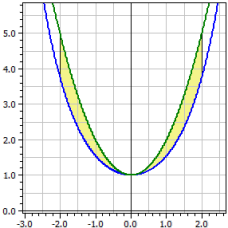
Example 2:

Arc length of the chain line compared to the normal parabola  y=x²+1.

  ƒ1(x) = cosh(x)
  ƒ2(x) = x^2+1

  Limits of integration from  -2  to  2

  Oriented content  :  A1 = -2,07961
  Absolute content  :  A2 = 2,07961

  Arc lengths          :  L1[a;b] = 7,254      L2[a,b] = 9,294 

Please note:

The integrals are determined using numerical methods. In principle, these reach their limits with functions with a very fast change of sign.

See also:

Supported Functions
Setting the graphics