Reihenentwicklung

Gezeichnet wird eine als Reihe  Σ ƒ(x,k)  gegebene Funktion, wobei die Reihenentwicklungen für verschiedene Parameterbereiche verglichen und zur besseren Unterscheidung in y-Richtung versetzt werden können.

Für k und natürlichzahlige Terme von k steht die Fakultät als Funktion fak(k) zur Verfügung, die bei vielen Reihenentwicklungen gebraucht wird.

Beispiel:

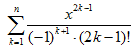ist eine Reihenentwicklung der Sinusfunktion.
 

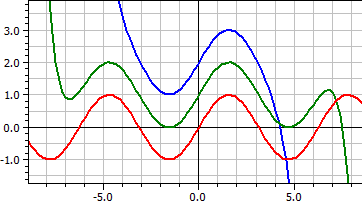
ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1)

ƒ1: k von 1 bis 4      verschoben um    dy = 2
ƒ2: k von 1 bis 8      verschoben um    dy = 1
ƒ3: k von 1 bis 16    verschoben um    dy = 0

Siehe auch:

Erlaubte Funktionsterme
Einstellen der Grafik
Wikipedia: Taylorreihe