Newton-Iteration

Bei der Newton-Iteration handelt es sich um ein Näherungsverfahren zur Berechnung einer Nullstelle von ƒ(x). Gibt man einen Startwert x₀ ein, der nahe genug an der gesuchten Nullstelle liegt, so wird als nächste Näherung x₁ der Schnitt der Tangente an den Graph von ƒ im Punkt P(x₀|ƒ(x₀)) mit der x-Achse berechnet.

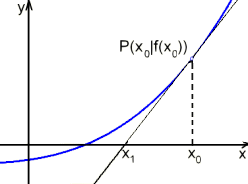
Dies führt auf die Rekursionsformel

    x_{n + 1}  = x_n  - ƒ (x_n) / ƒ '(x_n)

Das Verfahren konvergiert, wenn für x₀ gilt :
    ƒ(x₀) · ƒ "(x₀)>0.

Beispiel:

  ƒ(x) = x-cos(x)

                 x                       ƒ(x)                  ƒ'(x) 
   ————————   ——————   ——————   
   x0 = 1
   x1 = 0,75036387     0,45969769       1,841471
   x2 = 0,73911289     0,018923074     1,681905
   x3 = 0,73908513     0,00004646       1,6736325
   x4 = 0,73908513     0,00000000       1,673612

Siehe auch:

Erlaubte Funktionsterme
Wikipedia: Newton-Verfahren