Integralrechnung

Berechnet wird der orientierte und der absolute Inhalt der Fläche zwischen zwei Funktionskurven in einem gewünschten Intervall.

Außerdem werden bestimmt :

• die Drehmomente bei Drehung um die x- bzw. y-Achse,
• die dabei überstrichenen Rotationsvolumen,
• die Bogenlängen im Intervall [a;b] und
• der Schwerpunkt der Fläche (wenn A₁=A₂).

Beispiel 1:

  ƒ1(x) = 4-x^2
  ƒ2(x) = (x-1)^2

  Integrationsintervall  [a;b]  von  0 bis 3

  Orientierter Inhalt  :  A1 = 0,00000
  Absoluter Inhalt     :  A2 = 9,50675

  Drehmomente       :  Mx = 9                   My = -9

  Rotationsvolumen :  Vx = 56,5487         Vy = -56,5487

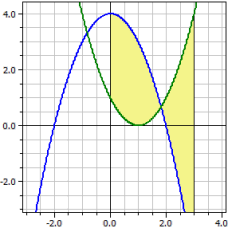
Beispiel 2:

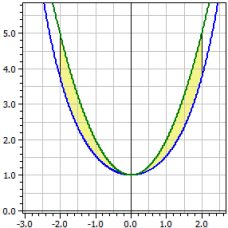
Bogenlänge der Kettenlinie verglichen mit der Normalparabel  y=x²+1.

  ƒ1(x) = cosh(x)
  ƒ2(x) = x^2+1

  Integrationsintervall  [a;b]  von  -2 bis 2

  Orientierter Inhalt  :  A1 = -2,07961
  Absoluter Inhalt     :  A2 = 2,07961

  Bogenlängen        :  L1[a;b] = 7,254    L2[a,b] = 9,294

Bitte beachten Sie:

Die Integrale werden mit numerischen Verfahren bestimmt. Diese stoßen bei Funktionen mit sehr schnellen Vorzeichenwechsel prinzipiell an ihre Grenzen.

Siehe auch:

Erlaubte Funktionsterme | Einstellen der Grafik
Wikipedia: Rotationskörper