Kurvendiskussion rationaler Funktionen
Das Programm führt für eine (gebrochen)rationale Funktion die Kurvendiskussion durch. Das heißt, es werden die Ableitungen, die Definitionslücken und stetige Fortsetzung bestimmt. Die Funktion wird auf Nullstellen, Extrema, Wendepunkte und das Verhalten für |x|→∞ untersucht. Die Schaubilder von ƒ, ƒ' und ƒ"; werden gezeichnet und eine Wertetabelle wird ausgegeben.
Die Koeffizienten des Zähler- und des Nenner-Polynoms können als Brüche, als gemischte Zahlen oder als abbrechende Dezimalzahlen eingegeben werden.
Alle Programmteile, in denen die Koeffizienten eines Polynoms eingegeben werden, haben ein Kontextmenü (rechte Maustaste), mit dem Sie die Eingaben aus einem Programmteil in die Zwischenablage kopieren und von dort in einem anderen Programmteil einfügen können.
Beispiel
Funktion :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Definitionslücken
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 Pol mit Vorzeichenwechsel
x =-2 Pol mit Vorzeichenwechsel
Ableitungen :
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
Nullstellen :
¯¯¯¯¯¯¯¯¯¯
N( 1 | 0 ) m = -0,916667
Extrema :
¯¯¯¯¯¯¯¯
H(-3,4641 |-3,64711 ) m = 0
T( 3,4641 | 4,14711 ) m = 0
Wendepunkte :
¯¯¯¯¯¯¯¯¯¯¯¯
W( 0 | 0,25 ) m = 0
Verhalten für |x|→∞
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Schiefe Asymptote y = 3/4·x + 1/4
Symmetrie
¯¯¯¯¯¯¯¯¯
Punktsymmetrisch zu W1( 0 | 0,25 )
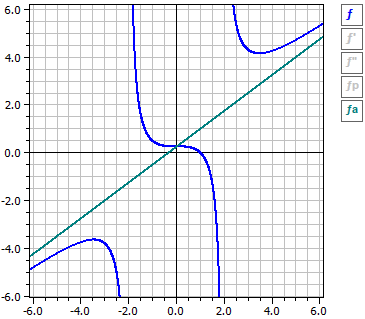
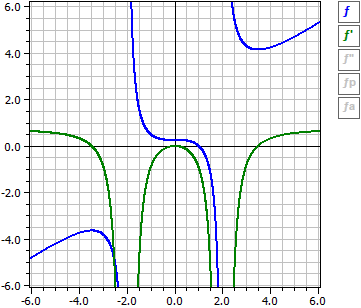
Mit den Schaltern am rechten Rand lassen sich die Kurven von ƒ, ƒ' und ƒ" sowie die Asymptoten bzw. Näherungskurven einzeln ein- und ausschalten.
Siehe auch:
Hinweise zum Verfahren | Erlaubte Funktionsterme | Einstellen der GrafikWikipedia: Rationale Funktion

