Kurvendiskussion ganzrationaler Funktionen

Das Programm führt für eine ganzrationale Funktion (Polynomfunktion) die Kurvendiskussion durch. Das heißt, es werden die Ableitungen und die Stammfunktion (Aufleitung) bestimmt, die Funktion wird auf rationale Nullstellen, auf Extrema, auf Wendepunkte und auf Symmetrie untersucht. Die Schaubilder von ƒ, ƒ' und ƒ" werden gezeichnet und eine Wertetabelle wird ausgegeben.

Die Koeffizienten des Polynoms können als Brüche, als gemischte Zahlen oder als abbrechende Dezimalzahlen eingegeben werden.

Werden Intervallgrenzen für ein Integral eingegeben, so wird zusätzlich zur Stammfunktion der Wert des bestimmten Integrals über diesem Intervall bestimmt.

Alle Programmteile, in denen die Koeffizienten eines Polynoms eingegeben werden, haben ein Kontextmenü (rechte Maustaste), mit dem Sie die Eingaben aus einem Programmteil in die Zwischenablage kopieren und von dort in einem anderen Programmteil einfügen können.

Beispiel: ƒ(x) = 3·x4 - 82/3·x2 + 3

Funktion :
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
       = 1/3·(9·x4 - 82·x2 + 9)
       = 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)

Ableitungen :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x)  = 12·x3 - 164/3·x
ƒ"(x)  = 36·x2 - 164/3
ƒ'"(x) = 72·x

Stammfunktion :
¯¯¯¯¯¯¯¯¯¯¯¯
F(x) = 3/5·x5 - 82/9·x3 + 3·x + c

Nullstellen :
¯¯¯¯¯¯¯¯¯¯
N1( 1/3 | 0)                             m = -17,7778
N2(-1/3 | 0)                             m =  17,7778
N3( 3 | 0)                                m =  160
N4(-3 | 0)                                m = -160

Extrema :
¯¯¯¯¯¯¯
H1( 0 | 3)                                m =  0
T1(-2,13437 |-59,2593)          m =  0
T2( 2,13437 |-59,2593)          m =  0

Wendepunkte :
¯¯¯¯¯¯¯¯¯¯¯
W1(-1,23228 |-31,5885)        m =  44,9098
W2( 1,23228 |-31,5885)        m = -44,9098

Symmetrie :
¯¯¯¯¯¯¯¯¯
Achsensymmetrisch zu a: x =0

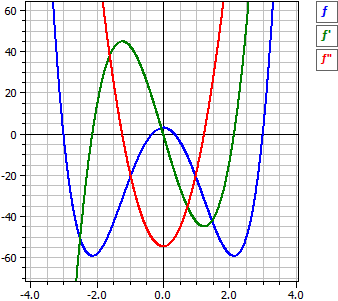
Mit den Schaltern am rechten Rand lassen sich die Kurven von ƒ, ƒ' und ƒ" einzeln ein- und ausschalten. 

   ƒ(x) = 3x⁴ - 82/3x² + 3

   x ∈ [ -10; 10 ],  Δx = 2

      x        ƒ(x)              ƒ'(x)            ƒ"(x)
 ——   —————  ————  ————— 
  -10       27269,7     -11453,3      3545,33
   -8        10541,7     -5706,67      2249,33
   -6        2907           -2264           1241,33
   -4        333,667     -549,333      521,333
   -2       -58,3333      13,3333      89,3333
    0         3                  0                -54,6667
    2        -58,3333     -13,3333      89,3333
    4         333,667      549,333      521,333
    6         2907           2264           1241,33
    8         10541,7      5706,67      2249,33
   10        27269,7      11453,3      3545,33

Siehe auch:

Hinweise zum Verfahren | Erlaubte Funktionsterme | Einstellen der Grafik
Wikipedia: Ganzrationale Funktion