Esempio 2: Pandemia di corona
Naturalmente, ha senso utilizzare i dati attuali sulla pandemia di corona per la regressione logistica. Ho preso i dati per la Germania dal sito Web della Johns Hopkins University (JHU) , che viene aggiornato quotidianamente e li ho salvati in due file CSV.
Dati da: "JHU_DE_Mrz-Apr.csv"
Limite di saturazione: 56 milioni
Figura scura: 1
4,559·1010
ƒ(x) = ——————————————
814,1 + 5,51·107·e^(-0,112·t)
Punto di svolta W(99,4|28 mio)
Tasso di crescita massimo ƒ'(xw) = 1.5688 mio
60 valori
Coefficiente di determinazione = 0,82574762
Coefficiente di correlazione = 0.90870656
Deviazione standard = 0.90673232
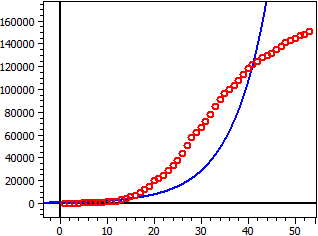
Germania marzo-aprile 2020, S=56 Mio, Figura scura=1.
Dati da: "JHU_DE_Mrz-Mai.csv"
Limite di saturazione: 56 Mio
Figura scura: 300
2,5497·1013
ƒ(x) = ——————————————————
4,553·105 + 5,5545·107 · e^(-0,10581·t)
Punto di svolta W(45,404/28 Mio)
Tasso di crescita massimo ƒ'(xw) = 1,4813 Mio
92 valori
Coefficiente di determinazione = 0,90140376
Coefficiente di correlazione = 0,94942285
Deviazione standard = 0,93956073
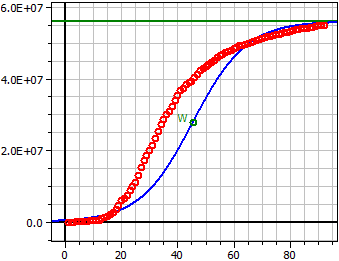
Germania marzo-maggio 2020, S=56 Mio, Figura scura=300.
Con valori elevati, il ridimensionamento cambia nel formato numerico scientifico. 4.0E+07 = 4.0·107 = 40.000.000 .
Ho assunto 56 milioni come limite di saturazione. Questo è il 70% di 80 milioni, il caso della presunta immunità del gregge .

