Modelli di crescita

La regressione riguarda la determinazione dei parametri sconosciuti di un modello di crescita o di una determinata funzione per una serie di dati di misurazione in modo tale che il modello finale si adatti ai dati nel miglior modo possibile.
I modelli considerati di frequente sono:

Crescita lineare

Con la crescita lineare, il tasso di crescita, ovvero la derivazione della funzione di crescita, è costante.
Il diagramma corrispondente è una linea retta.

Crescita esponenziale

Con una crescita esponenziale, il tasso di crescita è proporzionale alla popolazione :  ƒ'(t) ∼ ƒ(t)

Crescita limitata

Quando la crescita è limitata, il tasso di crescita è proporzionale al deficit di saturazione, ovvero quanto  è rimossa l'esistenza o il limite di saturazione S :  ƒ'(t) ∼ (S − ƒ(t))

Crescita logistica

Con la crescita logistica, si presume che l'inventario cresca essenzialmente in modo esponenziale all'inizio, ma che la crescita viene sempre più rallentata quando si avvicina il limite di saturazione. Si presume quindi che il tasso di crescita sia proporzionale allo stock e al deficit di saturazione. Ciò si traduce nell'equazione differenziale :   ƒ'(t) = k · ƒ(t) · (S − ƒ(t))
Questa ha la soluzione:

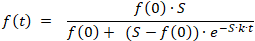
Metodo

Il programma determina la funzione logistica ƒ(t)  nella forma: 

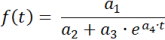
Quanto si applica ai parametri  a₁ = ƒ(0) · S ,  a₂ = ƒ(0) ,  a₃ = S - ƒ(0) , e  a₄ = k · S .

S   è il limite di saturazione, ovvero il valore a cui la funzione si avvicina in modo asintotico.
ƒ(0)  è il valore della funzione nel punto t=0  , che non deve corrispondere al primo valore misurato.

Inoltre, viene determinato il punto di svolta della funzione, ovvero il punto da cui la pendenza diminuisce nuovamente.
Il valore della funzione nel punto turno è sempre pari alla metà del limite di saturazione in modo ƒ(t_w ) = ½·S  .
La derivata ƒ'(t_w)  al punto di svolta fornisce il tasso di crescita massimo,

I parametri della funzione logistica sono determinati come segue:

1. Step: Forma la funzione reciproca di ƒ(t)   per ottenere la somma dal denominatore al numeratore.
2. Step: Prendi il logaritmo di entrambi i lati per ottenere l'esponente t .
3. Step: Portare l' equazione nella forma h (t) = m · t + b .
4. Step: Eseguire una regressione lineare per le coppie di valori (t | h(t) )
5. Step: Annullare la trasformazione per  m  e  b .

La regressione lineare fornisce anche il coefficiente di determinazione, il coefficiente di correlazione e la deviazione standard.