Regressione logistica
Il termine crescita logistica risale al matematico belga Pierre François Verhulst (1804-1849), che nel 1837 formulò la cosiddetta equazione logistica per descrivere gli sviluppi demografici.
Lo scopo del programma è di adattare la curva alla funzione logistica ƒ(t) per una serie di valori misurati.
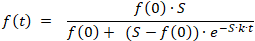
Oltre ai valori misurati, viene inserito un limite superiore stimato dei valori della funzione (limite di saturazione ).
Inoltre, è possibile inserire un fattore ( figura scura ), con il quale vengono moltiplicati i valori misurati,
se si assume che i valori effettivi siano superiori ai valori misurati per questo fattore.
Le coppie di valori possono essere immesse nella tabella o importate o esportate da un file in formato CSV (valori separati da virgola).
Per importare o esportare dati da un file CSV, aprire il menu contestuale facendo doppio clic con il pulsante destro del mouse sulla tabella.
Le voci di menu Eliminare dati , Copiare dati e Inserire dati corrispondenti alle funzioni Taglia , Copia e Incolla l'elaborazione del testo e li usa come appunti.
Esempio 1: Crescita del luppolo
Il luppolo, necessario per la produzione di birra, è una pianta rampicante in rapida crescita. Al fine di rilasciare dichiarazioni sulla crescita del luppolo, durante un'indagine sono state prese le seguenti serie di misurazioni.
| Tempo t (in settimane) |
0 | 2 | 4 | 6 | 8 | 10 | 12 | 16 |
| Altezza (in m) |
0,6 | 1,2 | 2,0 | 3,3 | 4,1 | 5,0 | 5,5 | 5,8 |
(Esempio da Lambacher Schweizer: Leistungskurs Analysis, Edition Baden-Wuerttemberg, 1st edition 2000)
Dati da: "hopfenwachstum.csv"
Limite di saturazione: 6
Numero non segnalato: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Punto di svolta W (5,8226|3)
Tasso di crescita massimo ƒ'(xw) = 0,53433
8 valori
Coefficiente di determinazione = 0.99383916
Coefficiente di correlazione = 0.99691482
Deviazione standard = 0,16172584
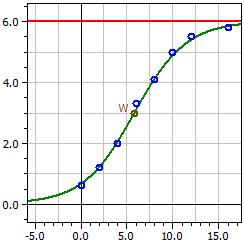
Come nel libro, il valore 6 è stato assunto come limite di saturazione. Tuttavia, i risultati differiscono da quelli del modello. Tuttavia, non viene eseguito alcun adattamento della curva, ma il fattore di proporzionalità k viene calcolato utilizzando qualsiasi coppia di dati, ad esempio con (12 | 5.5). I dati per questo esempio sono archiviati nel file Hopfenwachs.csv .
Vedi anche:
Esempio 2: Pandemia di corona | Regressione logistica - Metodo
Wikipedia: Equazione logistica | Pierre François Verhulst

