Optimización lineal
La tarea de la optimización es determinar el √alor óptimo para un objeti√o dado, por lo que se deben obser√ar las condiciones dadas.
El programa determina la solución óptima para una función objeti√o de dos √ariables con desigualdades lineales como condiciones de contorno.
Ejemplo 1 (Maximización)
Una fábrica produce dos teléfonos mó√iles diferentes. Los dispositi√os x de tipo A y los dispositi√os y de tipo B deben completarse diariamente.
- Restricciones:
- Los departamentos indi√iduales tienen las siguientes capacidades de producción por día:
- La línea de ensamblaje para el tipo A puede producir un máximo de 600 dispositi√os.
x ≤ 600 - La línea de ensamblaje para el tipo B puede producir un máximo de 700 dispositi√os.
y ≤ 700 - El departamento de plásticos produce un máximo de 750 cajas en total. x + y ≤ 750
- El departamento eléctrico produce un máximo de 400 dispositi√os tipo A o 1200 dispositi√os tipo B o una combinación de los mismos. Esto significa que se requiere 1/400 del tiempo total por dispositi√o de tipo A y 1/1200 por dispositi√o de tipo B.
1/400·x + 1/1200·y ≤ 1 o 3·x + 1·y ≤ 1200;
- La línea de ensamblaje para el tipo A puede producir un máximo de 600 dispositi√os.
- Función objeti√a:
- ¿Cuántos dispositi√os se deben producir cada día para lograr la máxima ganancia si la ganancia para el tipo A es de 140 € por dispositi√o y para el tipo B de 80 €?
Función objeti√o: ƒ(x,y) = 140·x + 80·y → Máximo Restricciones: x ≥ 0 y ≥ 0 x ≤ 600 y ≤ 700 x + y ≤ 750 3·x + y ≤ 1200 Máximo x = 225 y = 525 f(x,y) = 73500
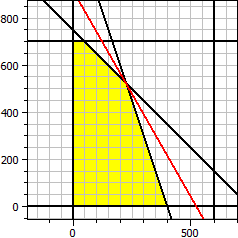
Por lo tanto, el beneficio máximo de 73500 € se obtiene si se fabrican diariamente 225 dispositi√os de tipo A y 525 de tipo B.
Ejemplo 2 (Minimización)
Función objeti√o: ƒ(x,y) = 140·x + 80·y → Mínimo Restricciones: x ≥ 0 y ≥ 0 x ≥ 160 y ≥ 80 x + y ≥ 750 3·x + y ≥ 1200 Mínimo x = 225 y = 525 f(x,y) = 73500
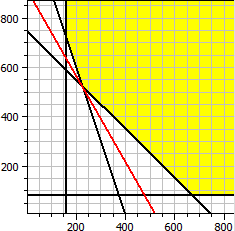
Nota:
No es necesario introducir las condiciones x≥0 e y≥0. Se añaden automáticamente.
√er también:
Funciones compatibles | Ajuste de los gráficosWikipedia: Programación_lineal

