Sistemas de ecuaciones lineales

El programa determina el vector solución de un sistema de ecuaciones lineales (SLE) con n ecuaciones y n variables.

Primero ingrese luego el número de ecuaciones y luego los coeficientes del sistema. El sistema debe transformarse para:

a_1,1 · x₁ + ... + a_1,n · x_n = b₁
  :           :
a_n,1 · x₁ + ... + a_n,n · x_n = b_n

Como resultado intermedio, se pueden informar la ref (Forma escalonada de fila) y el rref (Forma escalonada de hilera reducida).

Ejemplo con solución única:

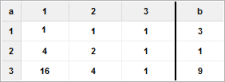
  1 · x1 + 1 · x2 + 1 · x3 = 3
  4 · x1 + 2 · x2 + 1 · x3 = 1
16 · x1 + 4 · x2 + 1 · x3 = 9

L = {(2; -8; 9;)}

Ejemplo con unidimensional solución:

 2 · x1 + 3 · x2 + 4 · x3 = 0
 1 · x1 - 1 · x2 - 1 · x3 = 1
 3 · x1 + 2 · x2 + 3 · x3 = 1

L = {(0,6-0,2t; -0,4-1,2t; t) | t ∈ R}        

Ejemplo con bidimensional solución:

 0 · x1 + 0 · x2 + 2 · x3 - 1 · x4 = 1
 1 · x1 + 1 · x2 + 1 · x3 + 1 · x4 = 4
 2 · x1 + 2 · x2 - 4 · x3 + 5 · x4 = 5
 1 · x1 + 1 · x2 - 7 · x3 + 5 · x4 = 0

L = {(3,5-s-1,5t; s; 0,5 + 0,5t; t) | s, t ∈ R}

Demostración del primer ejemplo:

Si busca a parábola a través de P(1|3), Q(2|1) y R(4|9), debe resolver el siguiente sistema de ecuaciones.

Enfoque:   ƒ(x) = a·x² + b·x + c

El vector solución es: (2,-8,9)

Por tanto, la parábola se describe mediante y = 2x² - 8x + 9.

Menú emergente:

Haga clic derecho para abrir un menú emergente, que le ofrece las siguientes funciones para administrar la matriz.

• Cortar matriz, copiar matriz  y pegar matriz

  Con esto puede copiar la matriz al portapapeles y pegarla en "Multiplicación de matrices".

• Exportar matriz e importar matriz

  Exports or imports the matrix in CSV format (Comma separated values), which is used to exchange data with Excel.