Estudio de funciones racionales
El programa realiza el boceto de la curva para una función racional (rota). Esto significa que se determinan las derivaciones y los vacíos en el dominio de definición. La función se examina para ceros, extremos, puntos de inflexión y el comportamiento de | x | &RArr; &Infin; Se dibujan los diagramas de ƒ, ƒ' y ƒ" y se genera una tabla de valores.
Los coeficientes del polinomio numerador y denominador se pueden ingresar como fracciones, como números mixtos o como números decimales finales.
Todas las partes del programa en las que se ingresan los coeficientes de un polinomio tienen un menú contextual (botón derecho del mouse) con el que puede copiar las entradas de una parte del programa al portapapeles y pegarlas desde allí en otra parte del programa.
Ejemplo
Función
¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = ———————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularidades
¯¯¯¯¯¯¯¯¯¯¯¯
x1 = 2 Polo con cambio de signo
x2 =-2 Polo con cambio de signo
Derivados
¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ————————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
Ceros
¯¯¯¯¯
N1( 1 | 0 ) m = -0,916667
Extrema
¯¯¯¯¯¯¯¯
H1(-3,4641 |-3,64711 ) m = 0
T1( 3,4641 | 4,14711 ) m = 0
Puntos de inflexión
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
W1( 0 | 0,25 ) m = 0
Comportamiento para |x| → ∞
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
asíntota oblicua y = 3/4·x + 1/4
Simetría
¯¯¯¯¯¯¯
Punto simétrico a W1( 0 | 0,25 )
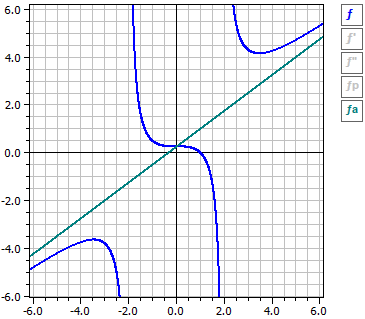
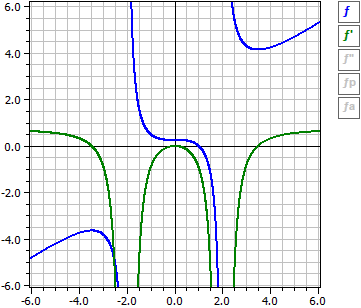
Con los interruptores en el borde derecho, las curvas de ƒ, ƒ' y ƒ", así como las asíntotas o curvas de aproximación se pueden activar y desactivar individualmente.
Ver también:
Notas sobre el procedimiento | Funciones compatibles | Ajuste de los gráficosWikipedia: Función racional

