Intersección de dos planos
Dados dos planos, el programa calcula la recta de intersección, la distancia de la línea desde el origen y el ángulo de intersección entre los dos planos.
Los planos se pueden ingresar en representación paramétrica o como ecuación de coordenadas
El programa traza la intersección de los planos en un cubo simétrico a los ejes y la recta de intersección de los dos planos.
Ejemplo 1:
Dados los dos planos:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1: 5·x - 2·y = 5
E2: 2·x - y + 5·z = 8
Línea de intersección:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧-11 ⎫ ⎧ 10 ⎫
g: x = ⎪-30 ⎪ + r·⎪ 25 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Distancia desde origen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d(g,O) = 1,5057283
Ángulo de intersección:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
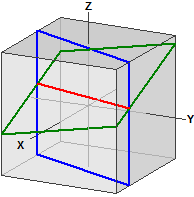
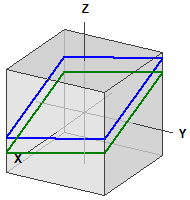
Ejemplo 2: Dos planos paralelos
Dados los dos planos: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E1: 2·x - y + 5·z = 12 E2: 2·x - y + 5·z = 0 Los planos son paralelos ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ d(E1,E2) = 2,1908902
El diagrama se puede desplazar con el botón izquierdo del mouse y ampliar con el botón derecho del mouse.

