Intersección de plano y recta
Dados un plano y una recta, se calculan el punto de intersección y el ángulo de intersección.
El plano se puede ingresar en representación paramétrica o como ecuación de coordenadas, la línea en representación paramétrica o por dos puntos.
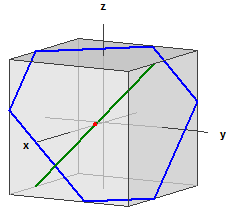
Ejemplo 1:
Plano E:
¯¯¯¯¯¯¯¯
E: x + y + z = 5
Recta g:
¯¯¯¯¯¯¯¯
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g: x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Punto de intersección :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S(5|0|0)
Ángulo de intersección:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 54,73561°
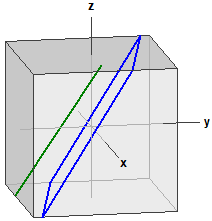
Ejemplo 2:
Plano E:
¯¯¯¯¯¯¯¯
E: 2·x + 8·y - 5·z = 0
Recta g:
¯¯¯¯¯¯¯¯
-> ⎧ 2 ⎫ ⎧ 1 ⎫
g: x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 2 ⎭
E y g son paralelos
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d(g,E) = -1,1406469
El diagrama se puede desplazar con el botón izquierdo del mouse y ampliar con el botón derecho del mouse.

