Intersección de dos rectas 3D
Dadas dos rectas, el programa calcula su punto de intersección, el ángulo de intersección y sus distancias desde el origen.
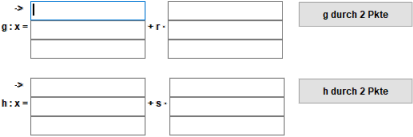
Las dos rectas se pueden dar en representación paramétrica o por dos puntos.
Si no tienen ningún punto común se calcula su distancia y los pies de la perpendicular común.
Ejemplo:
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g: x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h: x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
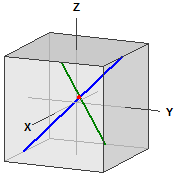
Punto de intersección de g y h: S (5|5|5)
Ángulo de intersección de g y h: 60°
Distancias desde origen:
d(O,g) = 5 d(O,h) = 5
Ejemplo con rectas oblicuas:
-> ⎧ 10 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩-1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 5 ⎭
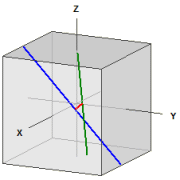
Las rectas no se cruzan
La distancia d (g,h) d(g,h) = 10,584755
Sedimentos de la perpendicular común :
F1(10|2,963|-2,963)
F2(-0,18519|5|-0,92593)
Distancias de origen :
d(O,g)=10 d(O,h)=5
El diagrama se puede desplazar con el botón izquierdo del mouse y ampliar con el botón derecho del mouse.

