Calculus of arbitrairy Functions

The program examines an arbitrary function ƒ. This means: The derivatives are determined; the function is investigated in regard of zeros, extremes (turning points) and inflection points for a previously defined range. The graphs of ƒ, ƒ', and ƒ" are plotted and a table of values is output.

Input

The function term is entered together with the range and the accuracy of examination and the angle mode.

The range is the interval in which the function is examined with respect of zeros, extremes and inflection points. It should not be too large, as this will increase the step size of the function check for sign reversal.

Output

The derivatives ƒ' and ƒ" of ƒ are determined by means of symbolic calculus according to the usual derivative rules. If problems arise, the derivatives can be switched off. Then the derivatives are calculated numerically. The differential quotients df(x)/dx are replaced by the difference quotients Δƒ(x)/Δx with a small Δx.

Zeros, local maxima, local minima and the inflection points of the function in the examined range are output.

Gaps in the domain of definition are not recognized by the program, simply because they often don't lie within the number domain or are skipped, due to the binary arithmetic. For this reason, extremes or inflection points can be indicated there by mistake.

What was told about the gaps in the domain of a definition is also valid for the continuity and for the existence of the derivatives of ƒ, ƒ' and ƒ". Inevitably, the user himself / herself will have to make some effort.

Example:

Function:
‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ(x) = x^4-2*x^3+1
  Examination in the range from -10  to  10

Derivatives:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ'(x) = 4*x^3-6*x^2
  ƒ"(x) = 12*x^2-12*x

Zeros:
‾‾‾‾‾‾‾‾
  N1(1|0)                     m = - 2
  N2(1,83929|0)          m = + 4,5912

Extremes:
‾‾‾‾‾‾‾‾‾‾‾‾‾
  T1(1,5|-0,6875)        m = 0

Inflection points:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  W1(0|1)                   m = + 0
  W2(1|0)                   m = - 2

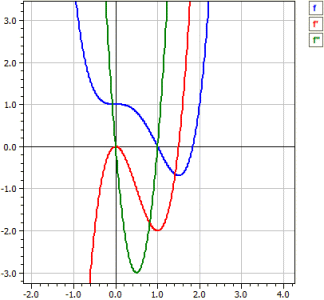
The curves of ƒ, ƒ' and ƒ" can be switched on and off individually using the switches on the right.

Table of Values:

Range and step of the table of values for ƒ, ƒ' and ƒ" can be defined here. Predefined is the examination range of the function. Places, where one of the functions is not defined, are marked by ---.

See also: