Calculus of Rational Functions
The program sketches the curve of a (broken) rational function. This means that the derivatives and the gaps in the domain of definition are determined. The function is examined for zeros, extremes (turning points), inflection points and the behavior for |x|→∞ The graphs of ƒ, ƒ' and ƒ" are drawn and a table of values is output.
The coefficients of the numerator and denominator polynomials can be entered as fractions, as mixed numbers or as terminating decimal numbers.
All parts of the program in which the coefficients of a polynomial are entered have a context menu (right mouse button) allows you to copy the entries from one program part to the clipboard and paste them from there into another program part.
Example
Function :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularities:
¯¯¯¯¯¯¯¯¯¯¯
x = 2 Pole with change of sign
x =-2 Pole with change of sign
Derivatives:
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = ————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ———————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
Zeros:
¯¯¯¯¯
N( 1 | 0 ) m = -0,916667
Extrema :
¯¯¯¯¯¯¯¯
H(-3,4641 |-3,64711 ) m = 0
T( 3,4641 | 4,14711 ) m = 0
Inflection points:
¯¯¯¯¯¯¯¯¯¯¯¯¯
W( 0 | 0,25 ) m = 0
Behavior for |x|→∞
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Oblique Asymptote y = 3/4·x + 1/4
Symmetry
¯¯¯¯¯¯¯¯¯
Centrally symmetric to W1( 0 | 0,25 )
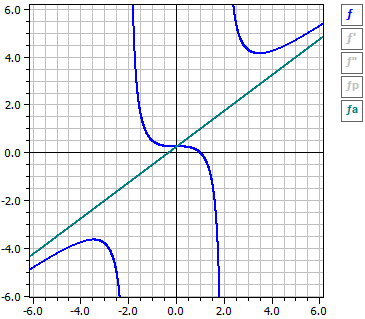
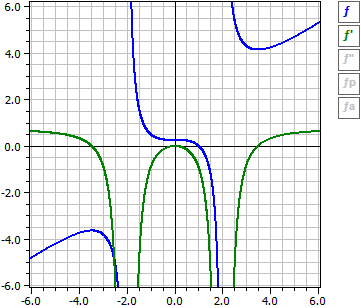
With the switches on the right side you can turn on and off the curves of ƒ, ƒ'and ƒ" as well as the asymptotes or approximation curves.
See also:
Notes on the procedure | Supported Functions | Setting the graphicsWikipedia: Rational function

