MatheAss 9.0 − Stochastik

Beispiel 2: Corona-Pandemie

Natürlich bietet es sich an, die aktuellen Daten zur Corona-Pandemie für eine logistische Regression heranzuziehen. Ich habe dazu der täglich aktualisierten Seite der Johns Hopkins University (JHU)  die Daten für Deutschland entnommen und in CSV-Dateien gespeichert. 

Daten aus:  "JHU_DE_Mrz-Apr.csv"

Sättigungsgrenze:  56 Mio
         Dunkelziffer:  1

                          4,559·1010
ƒ(x) = ——————————————
             814,1 + 5,51·107·e^(-0,112·t)

Wendepunkt W(99,4|28 Mio)

Maximale Wachstumsrate ƒ'(xw) = 1,5688 Mio  

60 Werte 
Bestimmtheitsmaß     = 0,82574762
Korrelationskoeff.       = 0,90870656
Standardabweichung = 0,90673232

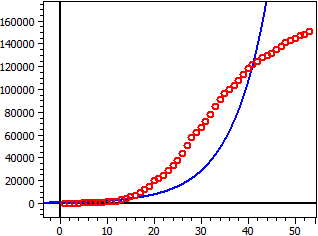
  Deutsche Corona-Zahlen März-April 2020, S=56 Mio, Dunkelziffer=1.

Daten aus: "JHU_DE_Mrz-Mai.csv"

Sättigungsgrenze: 56 Mio
         Dunkelziffer: 300

                            2,5497·1013
ƒ(x) = —————————————————
           4,553·105 + 5,5545·107 · e^(-0,10581·t)

Wendepunkt  W(45,404/28 Mio)

Maximale Wachstumsrate  ƒ'(xw) = 1,4813 Mio

92 Werte 
Bestimmtheitsmaß     = 0,90140376
Korrelationskoeff.       = 0,94942285
Standardabweichung = 0,93956073

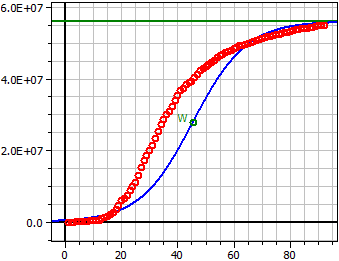
  Deutsche Corona-Zahlen März-Mai 2020, S=56 Mio, Dunkelziffer=300.

Die Skalierung wechselt bei großen Werten in das wissenschaftliche Zahlenformat. Dabei gilt: 4.0E+07 = 4,0·107 = 40 000 000.

Als Sättigungsgrenze habe ich 56 Mio. angenommen. Das sind 70% von 80 Mio, dem Fall der angeblichen Herdenimmunität.

Siehe auch:

Einstellen der Grafik