Wachstumsmodelle

Bei der Regression geht es darum, für eine Reihe von Messdaten die unbekannten Parameter eines Wachstumsmodells bzw. einer vorgegebenen Funktion so zu bestimmen, dass sich das endgültige Modell den Daten bestmöglich anpasst.
Häufig betrachtete Modelle sind:

Lineares Wachstum

Beim linearen Wachstum ist die Wachstumsrate, also die Ableitung der Wachstumsfunktion konstant.
Das zugehörige Schaubild ist eine Gerade.

Exponentielles Wachstum

Beim exponentiellen Wachstum ist die Wachstumsrate proportional zum Bestand.   ƒ'(t) ∼ ƒ(t)

Begrenztes Wachstum

Beim begrenzten Wachstum ist die Wachstumsrate proportional zum Sättigungsmanko, d.h., wie weit der Bestand noch von der Sättigungsgrenze S  entfernt ist.   ƒ'(t) ∼ (S − ƒ(t))

Logistisches Wachstum

Beim logistischen Wachstum geht man davon aus, dass der Bestand am Anfang im Wesentlichen exponentiell wächst, das Wachstum aber bei Annäherung an die Sättigungsgrenze immer mehr gebremst wird. Man nimmt also an, dass die Wachstumsrate sowohl zum Bestand als auch zum Sättigungsmanko proportional ist.
Daraus ergibt sich die Differentialgleichung:   ƒ'(t) = k · ƒ(t) · (S − ƒ(t))
mit der Lösung:

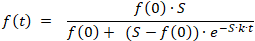
Verfahren

Das Programm bestimmt die Logistische Funktion ƒ(t )  in der Form: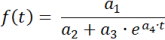 

Dabei gilt für die Parameter    a₁ = ƒ(0)·S ,  a₂ = ƒ(0) ,  a₃ = S − ƒ(0) ,  und  a₄ = −k·S .

S  ist die Sättigungsgrenze, das heißt der Wert, dem sich die Funktion asymptotisch annähert.
ƒ(0)  ist der Funktionswert an der Stelle t=0 , der nicht mit dem ersten Messwert übereinstimmen muss.

Außerdem bestimmt wird der Wendepunkt der Funktion, das heißt der Punkt, ab dem die Steigung wieder abnimmt.
Der Funktionswert an der Wendestelle ist immer gleich der Hälfte der Sättigungsgrenze also  ƒ(t_w) = ½·S .
Die Ableitung ƒ'(t_w)  an der Wendestelle liefert die maximale Wachstumsrate,

Die Parameter der Logistischen Funktion werden folgendermaßen ermittelt:

1. Schritt: Kehrwertfunktion von ƒ(t)  bilden, um die Summe vom Nenner in den Zähler zu bekommen.
2. Schritt: Beide Seiten logarithmieren, um an den Exponenten t  zu kommen.
3. Schritt: Die Gleichung auf die Form h(t) = m·t + b  bringen.
4. Schritt: Für die Wertepaare  ( t  | h(t)  )  eine Lineare Regression durchführen
5. Schritt: Für  m  und  b  die Transformation rückgängig machen.

Die Lineare Regression liefert auch das Bestimmtheitsmaß, den Korrelationskoeffizienten und die Standardabweichung.