Logistische Regression
Der Begriff Logistisches Wachstum geht zurück auf den belgischen Mathematiker Pierre François Verhulst (1804-1849), der 1837 die sogenannte Logistische Gleichung zur Beschreibung demografischer Entwicklungen formuliert hat.
Zweck des Programms ist es, zu einer Reihe von Messwerten eine Kurvenanpassung an die Logistische Funktion ƒ(t) durchzuführen.
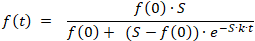
Neben den Messwerten werden dazu eine geschätzte obere Grenze der Funktionswerte (Sättigungsgrenze) eingegeben.
Außerdem kann ein Faktor (Dunkelziffer) eingegeben werden, mit dem die Messwerte multipliziert werden, wenn man davon ausgeht, dass die
die tatsächlichen Werte um diesen Faktor höher sind als die Messwerte.
Die Wertepaare können entweder in der Tabelle eingegeben oder aus einer Datei im CSV-Format (comma separated values) importiert bzw. exportiert werden.
Um Daten aus einer CSV-Datei zu importieren bzw. in diese zu exportieren, öffnen Sie das lokale Menü durch Doppelklick mit der rechten Maustaste auf die Tabelle.
Die Menüpunkte Daten löschen, Daten kopieren und Daten einfügen entsprechen den Funktionen Cut, Copy und Paste der Textverarbeitung und verwenden wie diese die Zwischenablage.
Beispiel 1: Hopfenwachstum
Hopfen, der zur Herstellung von Bier benötigt wird, ist eine schnell wachsende Schlingpflanze. Um Aussagen über das Hopfenwachstum zu machen, wurde bei einer Untersuchung die folgende Messreihe aufgenommen.
| Zeit t (in Wochen) |
0 | 2 | 4 | 6 | 8 | 10 | 12 | 16 |
| Höhe (in m) |
0,6 | 1,2 | 2,0 | 3,3 | 4,1 | 5,0 | 5,5 | 5,8 |
(Beispiel aus Lambacher Schweizer: Leistungskurs Analysis, Ausgabe Baden-WÜrttemberg, 1. Auflage 2000)
Daten aus: "Hopfenwachstum.csv"
Sättigungsgrenze: 6
Dunkelziffer: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Wendepunkt W(5,8226/3)
Maximale Wachstumsrate ƒ'(xw) = 0,53433
8 Werte
Bestimmtheitsmaß = 0,99383916
Korrelationskoeff. = 0,99691482
Standardabweichung = 0,16172584
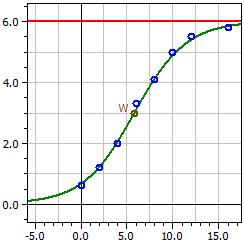
Als Sättigungsgrenze wurde wie im Buch der Wert 6 angenommen. Trotzdem weichen die Ergebnisse von denen der Vorlage ab. Dort wird allerdings keine Kurvenanpassung durchgeführt, sondern der Proportionalitätsfaktor k mithilfe eines beliebigen Datenpaares, z.B. mit (12|5,5), berechnet. Die Daten zu diesem Beispiel sind in der Datei Hopfenwachstum.csv gespeichert.
Siehe auch:
Beispiel 2: Corona-Pandemie | Logistische Regression - Verfahren
Wikipedia: Logistische Gleichung | Pierre François Verhulst

