Entfernungen auf der Kugel
Berechnet wird die Entfernung zwischen zwei Punkten P1 und P2 auf einer Kugel. Dabei werden eine Reihe von Funktionen von MatheAss zusammengefasst.
Eingegeben werden die GPS-Daten (Latitude und Longitude) der beiden Punkte. Zusammen mit dem Radius der Kugel ergeben sie die Polarkoordinaten der Punkte.
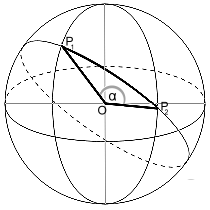
Diese werden mit der entsprechenden Funktion von MatheAss in ihre kartesischen Koordinaten umgerechnet. Das Ergebnis liefert die Koordinaten ihrer Ortsvektoren in einem Koordinatensystem mit dem Kugelmittelpunkt als Ursprung.
Mit ihrem Skalarprodukt erhält man den Winkel α zwischen den beiden Vektoren und schließlich als Produkt von α in Radiant mit dem Kugelradius die Länge des Kreisbogens auf der Kugel.
Beispiel:
Luftlinie zwischen dem Alexanderplatz in Berlin und der City Hall in New York.
Die Erde wird idealisiert als Kugel mit Radius 6371 km angenommen.
GPS dezimal
¯¯¯¯¯¯¯¯¯¯¯
Berlin : 52.523403, 13.4114
New York : 40.714268, -74.005974
GPS dms
¯¯¯¯¯¯¯
Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E
New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W
Polarkoordinaten
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlin : (6371 | 13,411400° | 52,523403°)
New York : (6371 |-74,005974° | 40,714268°)
Kartesische Koordinaten
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlin : (3770,6450 | 899,08721 | 5056,0379)
New York : (1330,5796 |-4642,1091 | 4155,7216)
Ortsvektoren
¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 3770,645048 ⎫ -> ⎧ 1330,57957098 ⎫
a = ⎪ 899,087213119 ⎪ b = ⎪-4642,10910614 ⎪
⎩ 5056,03788605 ⎭ ⎩ 4155,72160425 ⎭
-> ->
α = arccos( a · b / r2 )
= 1,002215 [rad] = 57,422692°
Entfernung
¯¯¯¯¯¯¯¯¯¯
d = r · α [rad] = 6385,112
Eingabe von GPS-Daten
GPS-Daten können sowohl dezimal als auch in Grad, Minuten und Sekunden eingegeben werden.
Ausgegeben werden beide Darstellungen.

Das Programm eignet sich damit auch zum Umrechnen von dezimalen Winkelmaßen in Grad, Minuten und Sekunden (dms) und umgekehrt.

