Koordinatensysteme
Mit diesem Programm lassen sich dreidimensionale kartesische Koordinaten in dreidimensionale Polarkoordinaten (Kugelkoordinaten) oder Zylinderkoordinaten umrechnen und umgekehrt.
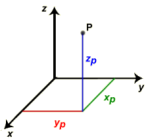
Kartesische_Koordinaten:
Die kartesischen Koordinaten (x|y|z) eines Punktes beziehen sich auf ein Koordinatensystem bei dem die Achsen senkrecht zueinander verlaufen und auf allen Achsen die gleiche Längeneinheit verwendet wird.
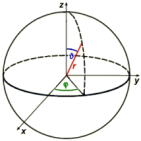
Polarkoordinaten:
Die Polarkoordinaten (r|φ|Θ) eines Punktes geben seinen Abstand r zum Ursprung an, den Drehwinkel φ (phi) in der Äquatorebene und den Erhebungswinkel Θ (Theta) aus der Äquatorebene heraus.
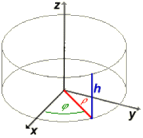
Zylinderkoordinaten:
Die Zylinderkoordinaten (rho|φ|z) eines Punktes geben seinen Abstand rho zur Zylinderachse an, den Drehwinkel φ (phi) um die Achse und die Höhe z über der xy-Ebene.
Beispiel:
kartesisch polar zylindrisch x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Mit z = 0 oder Θ = 0 erhält man zweidimenionale kartesische bzw. Polarkoordinaten.

