Ebene durch drei Punkte
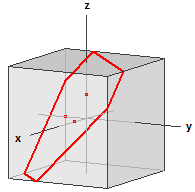
Drei Punkte im Raum, die nicht auf einer Geraden liegen, bestimmen genau eine Ebene. Gibt man die Koordinaten von drei Punkten ein, so bestimmt das Programm die Punkt-Richtungs-Form und die Koordinatengleichung der zugehörigen Ebene, sowie ihren Abstand vom Ursprung. Dabei werden die Richtungsvektoren und der Normalenvektor auf ganze Zahlen erweitert. Zusätzlich wird die Lage der Ebene im Raum durch ein Schrägbild veranschaulicht, das ihre Schnittgeraden mit einem achsensymmetrischen Würfel, sowie die Spurpunkte der Ebene enthält.
Beispiel
Ebene durch die Punkte:
A(1|2|3), B(2|3|3), C(1|0|1)
Punkt-Richtungs-Form:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Koordinatengleichung:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Abstand vom Ursprung:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Spurpunkte:
¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)