Das Oktaeder

Ein Oktaeder (Achtflach) ist eine regelmäßige vierseitige Doppelpyramide. Seine Oberfläche setzt sich aus acht kongruenten gleichseitigen Dreiecken zusammen. Damit gehört es zu den fünf Platonischen Körpern.

Von einem Oktaeder werden die folgenden Größen berechnet, wenn eine davon gegeben ist:

• Kante a
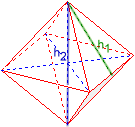
• Flächenhöhe h₁
• Raumhöhe h₂
• Umkugelradius r_u
• Inkugelradius r_i
• Volumen V
• Oberfläche O

Gegeben:
¯¯¯¯¯¯¯¯
Umkugelradius  ru = 1

Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
               Kante a = 1,4142136
  Flächenhöhe h1 = 1,2247449
     Raumhöhe h2 = 2
   Inkugelradius ri = 0,57735027
          Volumen V = 1,3333333
      Oberfläche O = 6,9282032

Gegeben:
¯¯¯¯¯¯¯¯
          Volumen V = 4/3

Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
               Kante a = 1,4142136
  Flächenhöhe h1 = 1,2247449
     Raumhöhe h2 = 2
Umkugelradius ru = 1	 
   Inkugelradius ri = 0,57735027
      Oberfläche O = 6,9282032

Siehe auch:

Wikipedia: Platonische Körper | Oktaeder | Formeln