Distanze sulla sfera
Viene calcolata la distanza tra due punti P1 e P2 su una sfera combinando alcune funzioni di MatheAss.
Vengono inseriti i dati GPS (latitudine e longitudine) dei due punti. Insieme al raggio della sfera, danno le coordinate polari dei punti.
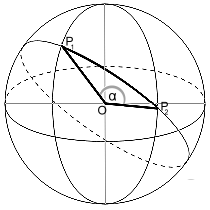
Questi vengono convertiti nelle loro coordinate cartesiane con la corrispondente funzione di MatheAss . Il risultato fornisce le coordinate dei loro vettori di posizione in un sistema di coordinate con il centro della sfera come origine.
Con il suo prodotto scalare si ottiene l'angolo α tra i due vettori e infine, come prodotto di α in radianti con il raggio sferico, la lunghezza dell'arco di cerchio sulla sfera.
Esempio:
In linea d'aria tra Alexanderplatz a Berlino e il municipio di New York.
La terra è idealizzata come una sfera con un raggio di 6371 km.
GPS decimali
¯¯¯¯¯¯¯¯¯¯¯
Berlino: 52.523403, 13.411400
New York: 40.714268, -74.005974
DMS GPS
¯¯¯¯¯¯¯
Berlino: 52° 31' 24.2508" N, 13° 24' 41.0400" E
New York: 40° 42' 51.3648" N, 74° 0' 21.5064" W
Coordinate polari
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlino: (6371 | 13,411400° | 52,523403°)
New York: (6371 |-74,005974° | 40,714268°)
Coordinate cartesiane
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Berlino : (3770,6450 | 899,08721 | 5056,0379)
New York : (1330,5796 |-4642,1091 | 4155,7216)
Vettori di posizione
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 3770,645048 ⎫ -> ⎧ 1330,57957098 ⎫
a = ⎪ 899,087213119 ⎪ b = ⎪-4642,10910614 ⎪
⎩ 5056.03788605 ⎭ ⎩ 4155.72160425 ⎭
-> ->
α = arccos( a · b / r2 )
= 1,002215 [rad] = 57,422692°
Distanza
¯¯¯¯¯¯¯¯
d = r · α [rad] = 6385,112
Inserimento dati GPS
I dati GPS possono essere inseriti sia in decimale che in gradi, minuti e secondi.
Entrambe le rappresentazioni vengono emesse.

Il programma è quindi adatto anche per convertire gradi decimali in gradi, minuti e secondi (dms) e viceversa.

