Sistemi di coordinate
Con questo programma, è possibile convertire le coordinate cartesiane tridimensionali in coordinate polari (coordinate sferiche) o coordinate cilindriche e viceversa.
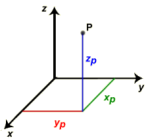
Coordinate cartesiane:
Le coordinate cartesiane (x | y | z) di un punto corrispondono a un sistema di coordinate con assi ortogonali e con la stessa misura su ciascun asse.
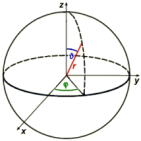
Coordinate polari:
Le coordinate polari (r | φ | θ) di un punto indicano la sua distanza r nell'origine, l'angolo di rotazione φ (phi) nella sezione equatoriale e l'angolo di elevazione Θ (Theta) nella sezione equatoriale.
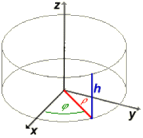
Coordinate cilindriche:
Le coordinate cilindriche (ρ | φ | z) di un punto indicano la sua distanza ρ (rho) dall'asse del cilindro, l'angolo di rotazione φ (phi) attorno all'asse e l'altezza z sull'origine.
Esempio:
cartesiano polare cilindrico x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Con z = 0 o Θ = 0 riceviamo coordinate bidimensionali.

