Intersezione di due rette (3D)
Il programma determina per due rette il punto di intersezione, l'angolo di intersezione e le distanze dall'origine.
Le righe devono essere immesse nella rappresentazione parametrica o con due punti.
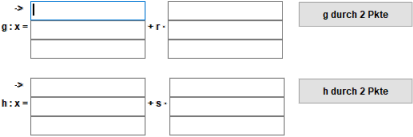
Se le rette non hanno un punto comune, vengono calcolate la loro distanza e i piedi della perpendicolare comune.
Esempio:
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
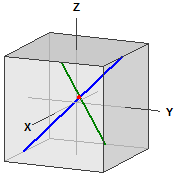
Punto di intersezione: S (5|5|5)
Angolo tra g e h: 60°
Distanze originali:
d(O,g) = 5 d(O,h) = 5
Esempio con rette a sinistra:
-> ⎧ 10 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩-1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 5 ⎭
Rettilinei sinistri
Distanza d(g,h) = 10.584755
Piedi della perpendicolare comune
F1 (10|2963|-2,963)
F2 (-0,18519|5|-0,92593)
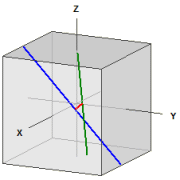
È possibile ruotare il diagramma con il tasto sinistro del mouse e ingrandire con il tasto destro del mouse.

