Optimisation linéaire
La tâche de l'optimisation consiste à déterminer la valeur optimale pour un objectif donné, selon laquelle des conditions données doivent être respectées.
Le programme détermine la solution optimale pour une fonction objectif à deux variables avec des inégalités linéaires comme conditions aux limites.
Exemple 1 (Maximisation)
Une usine produit deux téléphones portables différents. X appareils de type A et y appareils de type B sont à compléter quotidiennement.
- Contraintes:
- Les différents départements ont les capacités de production suivantes par jour :
- La chaîne de montage pour le type A peut produire un maximum de 600 appareils.
x ≤ 600 - La chaîne de montage pour le type B peut produire un maximum de 700 appareils.
y ≤ 700 - Le département plasturgie produit un maximum de 750 caisses au total. x + y ≤ 750
- Le département électrique produit un maximum de 400 appareils de type A ou 1200 appareils de type B ou une combinaison de ceux-ci. Cela signifie que 1/400 du temps total est requis par appareil de type A et 1/1200 par appareil de type B.
1/400·x + 1/1200·y ≤ 1 ou 3·x + 1·y ≤ 1200
- La chaîne de montage pour le type A peut produire un maximum de 600 appareils.
- Fonction objectif:
- Combien d'appareils doivent être produits chaque jour pour réaliser un profit maximum si le profit pour le type A est de 140 € par appareil et pour le type B de 80 €.
Fonction objectif: ƒ(x,y) = 140·x + 80·y → Maximum Contraintes: x ≥ 0 y ≥ 0 x ≤ 600 y ≤ 700 x + y ≤ 750 3·x + y ≤ 1200 Maximum: x = 225 y = 525 ƒ(x,y) = 73500
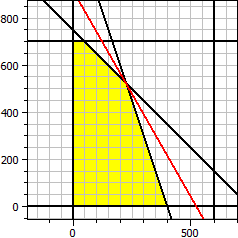
Le gain maximum de 73500 € est donc atteint si 225 appareils de type A et 525 de type B sont fabriqués quotidiennement.
Exemple 2 (Minimisation)
Fonction objectif: ƒ(x,y) = 140·x + 80·y → Minimum Contraintes: x ≥ 0 y ≥0 x ≥ 160 y ≥ 80 x + y ≥ 750 3·x + y ≥ 1200 Minimum: x = 225 y = 525 ƒ(x,y) = 73500
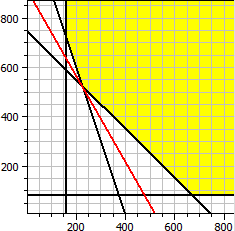
Remarque:
Les conditions x≥0 et y≥0 ne doivent pas être saisies. Elles sont ajoutées automatiquement.

