Systèmes d'équations linéaires

Le programme détermine le vecteur solution d'un seul système d'équation linéaire (SEL) avec n équation et n inconnues .

Le degré n et les coefficient du système d'équation sont entrés. D'abord le système d'équation doit-être transformé au :

a_1,1 ·x₁ + ... + a_1,n ·x_n = b₁

  :                                  :

a_n,1 ·x₁ + ... + a_n,n ·x_n = b_n

Comme un résultat intermédiaire la ref (Row Echelon Form) et la rref (Reduced Row Echelon Form) peuvent être signalés.

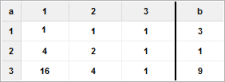
Exemple avec une seule solution:

 1·x1 + 1·x2 + 1·x3  =   3
 4·x1 + 2·x2 + 1·x3  =   1
16·x1 + 4·x2 + 1·x3  =   9

L = { ( 2; -8; 9; ) }

Example avec une solution unidimensionnelle:

 2·x1 + 3·x2 + 4·x3  =   0
 1·x1 - 1·x2 - 1·x3  =   1
 3·x1 + 2·x2 + 3·x3  =   1

L = { ( 0,6-0,2t; -0,4-1,2t; t ) | t ∈ R }}

Example avec une solution bidimensionnelle:

 0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
 1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
 2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
 1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Démonstration pour le premier exemple:

Si on cherche une parabole traversant les points  P(1|3), Q(2|1) and R(4|9), ça amène à :

L'approche:   f(x) = a·x² + b·x + c

avec le vecteur solution:     (2, -8, 9)

La parabole à alors l'équation   y = 2x² - 8x + 9.

Menu Pop-up:

Le menu contextuel (bouton droit de la souris) vous offre les fonctions suivantes pour traiter la matrice.

• Découper la matrice, Copier la matrice et Insérer la matrice

  Avec ça vous pouvez copier la matrice aux clipboard pour insérer par exemple à "Produit des matrices".

• Exporter la matrice ou Importer la matrice

  Exporter ou importer la matrice en format CSV (comma separated values), avec quel les données d'un fichier Excel peut être remplacé.