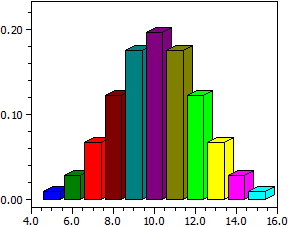
Distribution hypergéometrique

Pour une variable aléatoire X distribué de h(k;n;m;r) avec n,m et r donnés, le programme calcul un histogramme et une table de valeur pour les probalités P( X = k ).

La routine est particulièrement profitable. Il existe presqu'aucun tableau pour la distribution hypergéométrique et le calcul des probabilitées sont très laborieuses.

Théorie:

Une urne contient m boules, dans lesquelles r sont rouges. Si on tire n boules et sans les remettrent dedans, la variable aléatoire X indique combien de boules tirés sont rouges. La probabilité que k des boules tirées sont rouges est marquées avec P(X=k) = h(k,n,m,r).

On entre le nombre des boules tirées n, la totalité m et le nombre de boules rouges r. Car on tire sans les remettre dedans, il faut que n < m et r < m.

Exemple:

  n = 20;    m = 100;    r = 50

     k         P(X=k)            P(0 ≤ X < k)
  ——   ——————    ——————
     5       0,00889760      0,01141749 
     6       0,02780501      0,03922250 
     7       0,06613084      0,10535334 
     8       0,12160243      0,22695577 
     9       0,17460862      0,40156439 
    10      0,19687122      0,59843561 
    11      0,17460862      0,77304423 
    12      0,12160243      0,89464666 
    13      0,06613084      0,96077750 
    14      0,02780501      0,98858251 
    15      0,00889760      0,99748011 
  ——   ——————    ——————
  P(5 ≤ k < 15) =             0,99496023