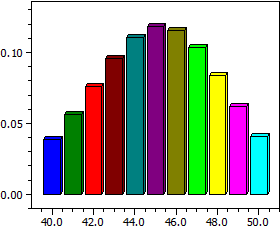
Distribution binomiale

Pour une variable aléatoire X distribué de b(k;n;p) avec n et p donnés, le programme calcul:

• un histogramme des probabilités P( X = k )
• leurs valeurs numériques dans un intervalle [ k_min; k_max]
• la probabilité P( k_min ≤ X ≤ k_max)

Théorie:

D'une urne avec une part de p boules rouges on tire n boules et elles sont remisent dedans. La variable aléatoire X indique combien de boules tirées sont rouges. La probabilité que k des boules tirées sont rouges est marquées avec P(X=k) = b(k;n;p).

On entre les valeurs de n et p, cependant p comme probabilité doit être entré 0 et 1. Après cela un histogramme simple donne un aperçu des valeurs de P(X = k). Dans une table des valeurs, les valeurs numérique sont listées.

Exemple:

  n = 60;    p = .75

     k           P(X=k)          P(0 ≤ X < k)
  ——    ——————   ——————
    40      0,03834033      0,09248427 
    41      0,05610780      0,14859207 
    42      0,07614630      0,22473838 
    43      0,09562559      0,32036397 
    44      0,11083875      0,43120273 
    45      0,11822800      0,54943073 
    46      0,11565783      0,66508856 
    47      0,10335381      0,76844237 
    48      0,08397497      0,85241733 
    49      0,06169589      0,91411323 
    50      0,04071929      0,95483252 
  ——    ——————   ——————
  P(40 ≤ k < 50) =           0,90068858

Voir aussi:

Wikipedia: Loi binomiale