Distribution normale

Pour une variable aléatoire X distribuée de N(μ,σ²) avec l'estimation μ et la variante  σ², le programme trace

 

- la fonction de densité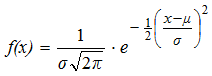    

- la fonction de distribution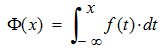  

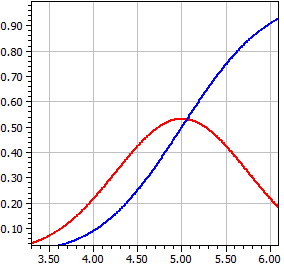
Le diagramme de la fonction de densité f est souvent appelé comme courbe de Gauss ou de courbe en cloche à cause de sa forme. La fonction de distribution f est appelée fonction d'erreurs de Gauss parce qu'on approuve cette distribution pour des erreurs accidentelles dans les observations astronomiques.

On entre l'estimation  μ  et la variante  σ². Pour  μ=0  et  σ=1  on reçu la distribution normale réduite.

Exemple:

  μ = 5 ,      σ = .75

         x                     ƒ(x)                   Φ(x)      
  —————       –—————     —————–
  2                       0,00017844      0,00003167   
  2,33333333      0,00095649      0,00018859
  2,66666666      0,00420802      0,00093192
  2,99999999      0,01519465      0,00383038
  3,33333332      0,04503153      0,01313415
  3,66666665      0,10953585      0,03772017
  3,99999998      0,21868009      0,09121120
  4,33333331      0,35832381      0,18703139
  4,66666664      0,48189843      0,32836063
  4,99999997      0,53192304      0,49999998
  5,3333333        0,48189845      0,67163934
  5,66666663      0,35832383      0,81296859
  5,99999996      0,21868012      0,90878878
  6,33333329      0,10953586      0,96227982

Voir aussi:

Ajuster des graphiques
Wikipedia: Loi normale