Des modèles de croissance
La régression consiste à déterminer les paramètres inconnus d'un modèle de croissance ou d'une fonction donnée pour une série de données de mesure de telle sorte que le modèle final s'adapte au mieux aux données.
Les modèles fréquemment considérés sont:
- Croissance linéaire
- Avec une croissance linéaire, le taux de croissance, c'est-à-dire la dérivation de la fonction de croissance, est constant.
Le diagramme correspondant est une ligne droite. - Croissance exponentielle
- Avec une croissance exponentielle, le taux de croissance est proportionnel à la population. ƒ'(t) ∼ ƒ(t)
- Croissance limitée
- Lorsque la croissance limitée, le taux de croissance est proportionnelle au déficit de saturation, qui est dans quelle mesure l'existence ou de la limite de saturation S est supprimé. ƒ'(t) ∼ (S − ƒ(t))
- Croissance logistique
- Avec la croissance logistique, on suppose que l'inventaire croît essentiellement de façon exponentielle au début,
mais que la croissance se ralentit de plus en plus à mesure que la limite de saturation approche. On suppose donc que
le taux de croissance est proportionnel à la fois au stock et au déficit de saturation. Il en résulte l'équation différentielle:
ƒ'(t) = k · ƒ(t) · (S − ƒ(t))
Cela a la solution: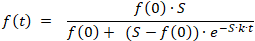
La méthode
Le programme détermine la fonction logistique f (t) sous la forme:
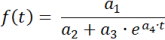
Les paramètres sont a1 = f(0)·S , a2 = f(0) , a3 = S - f(0) et a4 = -k·S .
S est la limite de saturation, c'est-à-dire la valeur que la fonction approche de manière asymptotique.
f(0) est la valeur de la fonction au point t = 0 , qui ne doit pas nécessairement correspondre à
la première valeur mesurée.
De plus, le point d'inflexion de la fonction est déterminé, c'est-à-dire le point à partir duquel la pente va diminuer.
La valeur de la fonction au point d'inflexion est toujours égale à la moitié de la limite de saturation si
f(tw ) = ½·S .
La dérivée f 'tw ) au point d'inflexion fournit le taux de croissance maximum,
Les paramètres de la fonction logistique sont déterminés comme suit:
- Étape: Formez la fonction réciproque de f(t) pour obtenir la somme du dénominateur au numérateur.
- Étape: Prendre le logarithme des deux côtés pour obtenir l'exposant t .
- Étape: Formez l'équation à la forme h(t) = m·t + b .
- Étape: Fais une régression linéaire pour les paires de valeurs ( t | h(t) )
- Étape: Defair la transformation pour m et b .
La régression linéaire fournit également le coefficient de détermination, le coefficient de corrélation et l'écart type.

