Exemple 2: Pandémie de Corona
Bien sûr, il est logique d'utiliser les données actuelles sur la pandémie corona pour la régression logistique.
J'ai pris les données pour l'Allemagne sur le site Web de l'Université Johns Hopkins (JHU) , qui est mis à jour quotidiennement ,
et les ai sauvé dans deux fichiers CSV. L'un, JHU_DE_Mrz.csv, contient les données de mars 2020, le deuxième JHU_DE_Mrz-Apr.csv que j'ai continué à maintenir.
Données de: "JHU_DE_Mrz-Apr.csv"
Limite de saturation: 56 Mio
Figure sombre: 1
4,559·1010
ƒ(x) = ——————————————
814,1 + 5,51·107·e^(-0,112·t)
Point d'inflexion W(99,4/28 Mio)
Taux de croissance maximal ƒ'(xw) = 1,5688 Mio
60 valeurs
Coeff. de déterm. = 0,82574762
Coeff. de correl. = 0,90870656
Ecart-type = 0,90673232
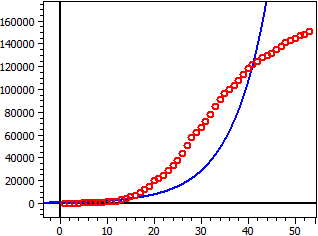
Dates du mars au avril 2020, S=56 Mio, Figure sombre=1
Données de: "JHU_DE_Mrz-Mai.csv"
Limite de saturation: 56 Mio
Figure sombre: 300
2,5497·1013
ƒ(x) = ——————————————————
4,553·105 + 5,5545·107 · e^(-0,10581·t)
Point d'inflexion W(45,404/28 Mio)
Taux de croissance maximal ƒ'(xw) = 1,4813 Mio
60 valeurs
Coeff. de déterm. = 0,90140376
Coeff. de correl. = 0,94942285
Ecart-type = 0,93956073
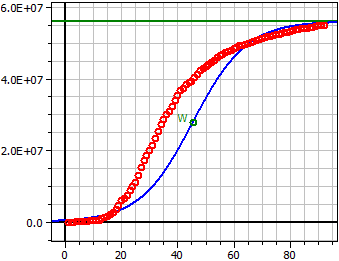
Dates du mars au mai 2020, S=56 Mio, Figure sombre=300.
Avec de grandes valeurs, la mise à l'échelle passe au format numérique des nombres.
J'ai supposé 56 millions comme limite de saturation. Cela représente 70% des 80 millions, le cas d'une prétendue immunité grégaire.

