Intersection de deux sphères
Si les coordonnées des centres et les rayons des deux sphères sont donnés, le programme détermine le centre et le rayon du cercle d'intersection, ainsi que l'équation en coordonnées du plan d'intersection.
Si vous entrez Zéro comme rayon d'une sphère et un point sur l'autre sphère pour centre, vous reçevez une équation de plan tangeant.
Exemple:
Les deux sphères: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Le cercle d'intersection: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2) , r = 2,4494897 Le plan d'intersection: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
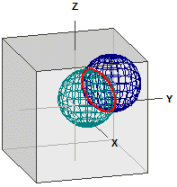
Vous pouvez tourner le diagramme avec le bouton gauche de la souris et faire un zoom avec le bouton droit de la souris.

