Intersection de deux plans
Pour deux plans, le programme détermine la droite d'intersection, la distance d'origine de la droite et l'angle entre les deux plans.
Les plans peuvent être être entrées en représentation paramétrique ou en équation coordonnées
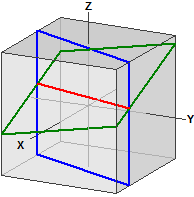
Les intersections du plan avec un cube symétrique aux axes et la droites d'intersection des deux plans sont désigné.
Exemple 1:
Les deux plans:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
La droite d'intersection:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧-11 ⎫ ⎧ 10 ⎫
g : x = ⎪-30 ⎪ + r·⎪ 25 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
La distance de l'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
L'angle entre les plans:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alpha = 65,993637°
Exemple 2:
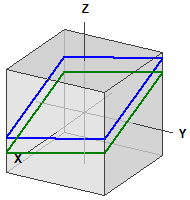
Les deux plans: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E1 : 2·x - y + 5·z = 12 E2 : 2·x - y + 5·z = 0 Les plans sont parallèles ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ d(E1,E2) = 2,1908902
Vous pouvez tourner le diagramme avec le bouton gauche de la souris et faire un zoom avec le bouton droit de la souris.

