Intersection de plan et droite
Le programme détermine pour un plan et une droite le point d'intersection et l'angle d'intersection.
Le plan peut être être entrées en représentation paramétrique ou en équation coordonnées, la droite en représentation paramétrique ou par deux points.
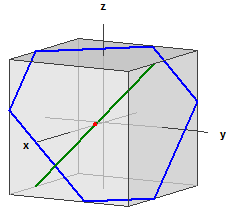
Exemple 1:
Le plan E :
¯¯¯¯¯¯¯¯¯¯¯¯
E : x + y + z = 5
La droite g :
¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Le point d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S(5|0|0)
L'angle d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 54,73561°
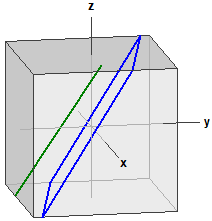
Exemple 2:
Le plan E :
¯¯¯¯¯¯¯¯¯¯¯¯
E : 2·x + 8·y − 5·z = 0
La droite g :
¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 2 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 2 ⎭
E et g sont parallèles
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d(g,E) = -1,1406469
Vous pouvez tourner le diagramme avec le bouton gauche de la souris et faire un zoom avec le bouton droit de la souris.

