Producto vectorial
Dados dos vectores, se calculan el producto vectorial y su magnitud.
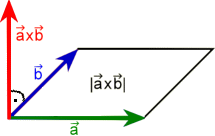
El producto vectorial es un vector ortogonal al paralelogramo que representan los vectores dados. Su magnitud es igual al área del paralelogramo.
Ejemplo:
-> ⎧ 1 ⎫ -> ⎧ 7 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 4 ⎭
-> -> ⎧ 5 ⎫ -> ->
a x b = ⎪ 17 ⎪ | a x b | = 21,977261
⎩-13 ⎭
Solicitud:
Suponga que se va a calcular el área del triángulo con las esquinas A(0|0|0), B(1|2|3) y C(7|1|4).
El triángulo es la mitad del paralelogramo atravesado por los dos vectores del ejemplo. Por lo tanto, su área es la mitad de su producto vectorial A ≈ 11 UA.

