Distribución normal

Para una variable aleatoria X distribuida N(μ, σ² ) con un valor esperado μ dado y una varianza σ² , puede calcular

 

- la función de densidad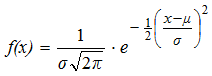      

- y la función de distribución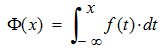

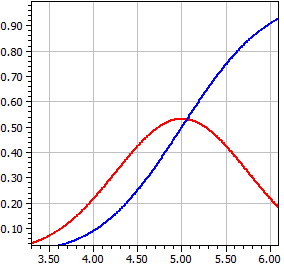
El diagrama de la función de densidad ƒ(x) a menudo se denomina curva gaussiana o curva en forma de campana. La función de distribución Φ(x) se designa como función de error de Gauss, porque, según Gauss, esta distribución se supone para los errores aleatorios en las observaciones astronómicas.

Se ingresan el valor esperado μ y la varianza σ² . Para μ = 0 y σ = 1, recibe la distribución normal estandarizada.

Ejemplo:

  μ = 5, σ = .75

         x                 ƒ(x)                 Φ(x)      
  —————— —————— ——————
  2 0,0001784   0,00003167     
  2,33333333    0,00095649    0,00018859
  2,66666666    0,00420802    0,00093192
  2,99999999    0,01519465    0,00383038
  3,33333332    0,04503153    0,01313415
  3,66666665    0,10953585    0,03772017
  3,99999998    0,21868009    0,09121120
  4,33333331    0,35832381    0,18703139
  4,66666664    0,48189843    0,32836063
  4,99999997    0,53192304    0,49999998
  5,3333333      0,48189845    0,67163934
  5,66666663    0,35832383    0,81296859
  5,99999996    0,21868012    0,90878878
  6,33333329    0,10953586    0,96227982

Ver también:

Ajuste de los gráficos
Wikipedia: Distribución normal