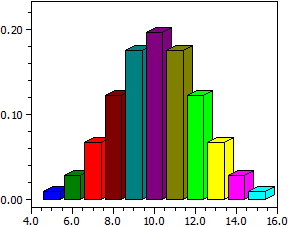
Distribución hipergeométrica

Para un h(k;n;m;r) variable aleatoria distribuida X con n, m y r fijos, puede calcular un histograma y una tabla de valores para las probabilidades P (X = k).

Esta rutina es especialmente útil, porque casi no existen tablas de distribución hipergeométrica debido a las cuatro variables de entrada, y el cálculo de probabilidades requiere un gran gasto.

Teoría:

Un recipiente está lleno de m bolas, r de las cuales son rojas. Si se extraen n bolas sin reemplazo, entonces la variable aleatoria X indica cuántas bolas rojas se extrajeron. La probabilidad de que k de las bolas extraídas sean rojas se caracteriza por P(X = k) = h(k,n,m,r).

Se ingresan la cantidad de bolas extraídas n, la cantidad total my la cantidad de bolas rojas r. a medida que avanza el dibujo sin descartar, verifique que n<m, y también r<m.

Ejemplo:

  n = 20; m = 100; r = 50

     k      P(X = k)        P(0 ≤ X <k)
  —— —————— ——————
      5    0,00889760   0,01141749 
      6    0,02780501   0,03922250 
      7    0,06613084   0,10535334 
      8    0,12160243   0,22695577 
      9    0,17460862   0,40156439 
    10    0,19687122   0,59843561 
    11    0,17460862   0,77304423 
    12    0,12160243   0,89464666 
    13    0,02780501   0,98858251 
    15    0,00889760   0,99748011 
  —— —————— ——————
  P (5 ≤ k <15) =        0,99496023

Ver también:

Distribución hipergeométrica