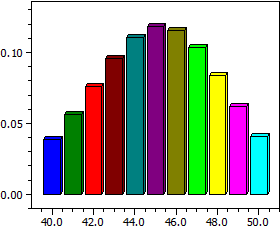
Distribución binomial

Para ab (k; n; p) variable aleatoria distribuida X con n y p fijos, puede calcular

• un histograma de las probabilidades P(X = k)
• una tabla de sus valores de k_min a k_max
• la probabilidad P(k_min < X < k_max )

Teoría:

Se extraen n bolas con reemplazo de un recipiente con una porción p de bolas rojas. La variable aleatoria X representa la cantidad de bolas rojas extraídas. La probabilidad de que k de las bolas extraídas sean rojas se caracteriza por P(X=k) = b(k; n; p).

Se ingresan los valores para n y p, donde p como probabilidad tiene que estar entre 0 y 1. Después de esto, un histograma simple da una primera encuesta sobre los valores de P(X=k). Los valores numéricos se emiten en una tabla de valores.

Ejemplo:

  n = 60; p = 0,75

     k     P(X = k)         P(0 ≤ X <k)
  —— —————— ——————
    40   0,03834033   0,09248427 
    41   0,05610780   0,14859207 
    42   0,07614630   0,22473838 
    43   0,09562559   0,32036397 
    44   0,11083875   0,43120273 
    45   0,11822800   0,54943073 
    46   0,11565783   0,66508856 
    47   0,10335381   0,76844237 
    48   0,08397497   0,8524­3 
    49   0,06169589   0,91411323 
    50   0,04071929   0,95483252 
  —— —————— ——————
  P (40 ≤ k <50) =     0,90068858

Ver también:

Wikipedia: Distribución binomial