Transformación de polinomios
Un polinomio p (x) se puede desplazar o estirar en la dirección x y en la dirección y.
p (x) = a9·x9 + a8·x8 + ... + a0 .
Los coeficientes del polinomio se pueden ingresar como fracciones, como números mixtos o como números decimales de ruptura.

ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Desplazado por dx = -2, dy = 0 ƒ(x + 2) = - 1/4·x4 + 6·x2 + 1
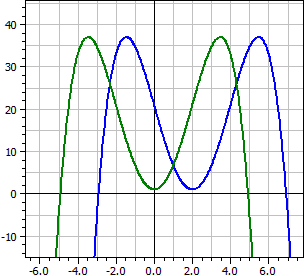
En el ejemplo, la función ƒ(x) tiene el eje de simetría a: x = 2 al desplazar 2 unidades hacia la izquierda obtenemos la función ƒ(x + 2), que es simétrica al eje y. Por lo tanto, solo tiene sumandos con potencias pares de x.
Intercambio de datos a través del portapapeles de Windows
Todas las partes del programa en las que se ingresan los coeficientes de un polinomio tienen un menú contextual (botón derecho del mouse) con el que puede copiar las entradas de una parte del programa al portapapeles y pegarlas desde allí en otra parte del programa.
Los coeficientes de la función transformada se copian automáticamente en el portapapeles.
De esta manera, las funciones ƒ(x) y ƒ(x + 2) se copiaron y pegaron en el trazador de funciones de parte del programa. La función pegar convierte automáticamente la tabla de coeficientes en el término de la función.
Más ejemplos:
ƒ(x) = x5 + 10·x4 + 36·x3 + 56·x2 + 33·x + 3 Desplazado por dx = 2, dy = 1 ƒ(x -2) + 1 = x5 - 4·x3 + x + 2
ƒ(x) = 1/4·x4 + 2·x2 - 1 Estirado por sx = 2, sy = 1 ƒ(1/2·x) = 1/64·x4 + 1/2·x2 - 1
ƒ(x) = 1/4·x4 + 2·x2 - 1 Estirado por sx = 1/2, sy = 3 3·ƒ(2·x) = 12·x4 + 24·x2 - 3
ƒ(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 Estirado por sx = -1, sy = 9 9·ƒ(-1x) = - 9·x5 - 81·x4 + 246·x3 + 738·x2

