Plano a través de tres puntos

Tres puntos no colineales determinan exactamente un plano. Dadas las coordenadas de tres puntos, el programa calcula la ecuación de este plano en forma punto-pendiente y en forma de coordenadas, así como su distancia desde el origen con los vectores direccionales y los vectores normales incrementados a números enteros. además de esto, se traza la posición del plano en el área, incluidas sus líneas que cortan un cubo simétrico a los ejes, así como sus puntos de traza.

Ejemplo:

Plano por los puntos:
A(1|2|3), B(2|3|3), C(1|0|1)

Forma de punto-pendiente:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
->  ⎧ 1 ⎫     ⎧ 1 ⎫     ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
    ⎩ 3 ⎭     ⎩ 0 ⎭     ⎩ 1 ⎭

Ecuación en coordenadas:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2

Distancia desde origen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005

Puntos de seguimiento:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0), Sy(0|-2|0), Sz(0|0|2)

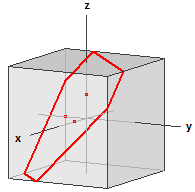
El diagrama se puede desplazar con el botón izquierdo del mouse y ampliar con el botón derecho del mouse.

Ver también:

Gráficos 3D
Wikipedia: Plano